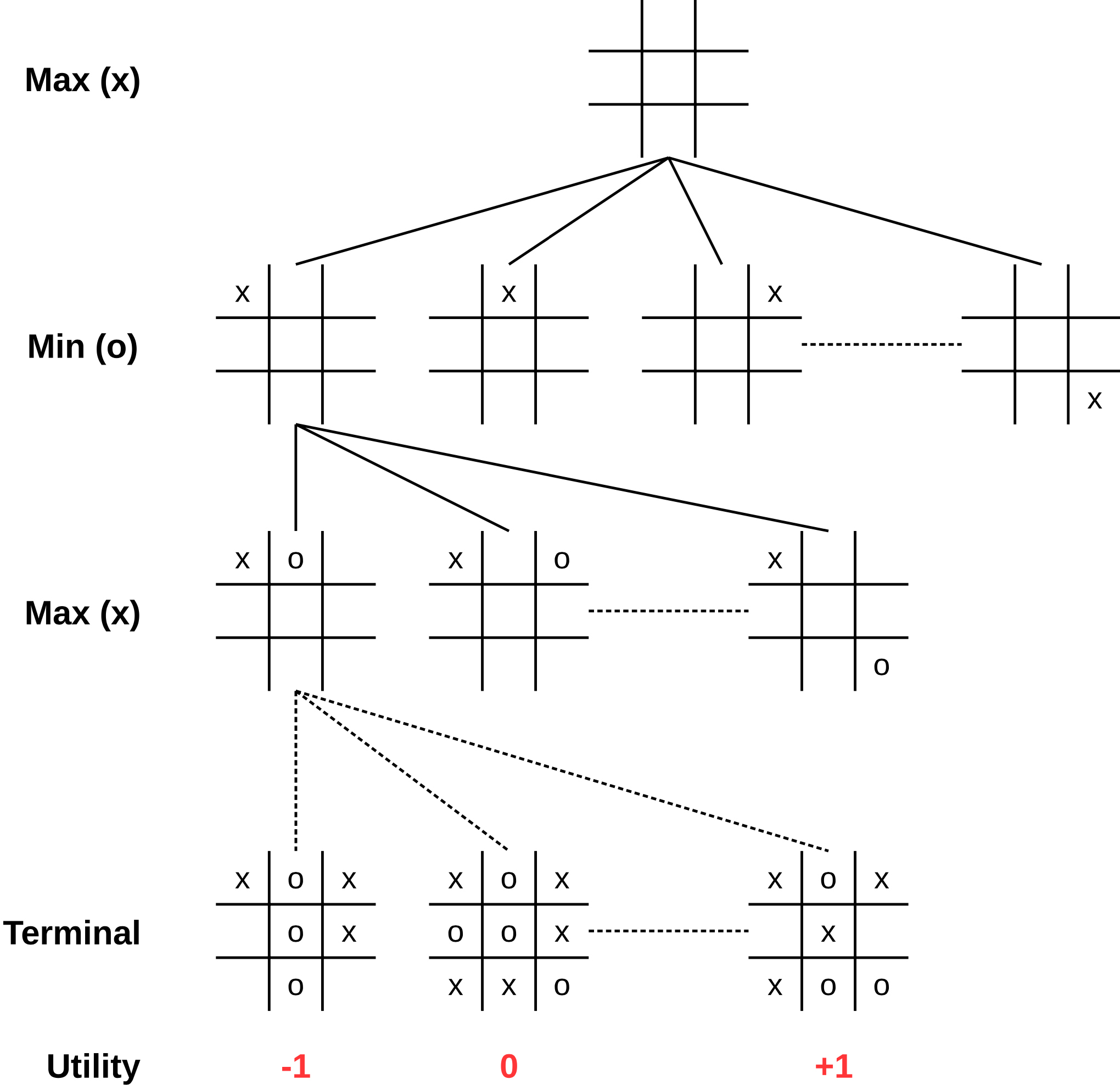
Minimax

Spiele als Suchproblem: Minimax

Terminologie

• Zwei abwechselnd spielende Spieler: MAX und MIN, wobei MAX beginnt

  • Beide Spieler spielen in jedem Zug optimal
  • Spielergebnis wird aus Sicht von MAX bewertet:
    • $+1$, wenn Spieler MAX gewinnt
    • $-1$, wenn Spieler MIN gewinnt
    • $0$, wenn unentschieden
  • Spieler MAX versucht, das Spielergebnis zu maximieren
  • Spieler MIN versucht, das Spielergebnis zu minimieren

• Startzustand: Initialer Zustand des Spielbrettes

• Aktionen: Legale Züge, abhängig vom Spielzustand

• Zieltest: Ist das Spiel vorbei?

  => Startzustand und anwendbare Aktionen definieren den Zustandsraum.

• Nutzenfunktion: $\operatorname{UTILITY}(s,p)$: Wert des Spiels für Spieler $p$ im Spielzustand $s$

• Strategie: Spieler benötigen Strategie, um zu gewünschtem Endzustand zu kommen (unabhängig von den Entscheidungen des Gegenspielers) => einfacher Pfad von Start zu Ziel reicht nicht

Hinweis: Nullsummenspiel! (Der Gewinn des einen Spielers ist der Verlust des anderen Spielers.)

Eine mit dem Minimax-Algorithmus berechnete Strategie wird auch Minimax-Strategie genannt. Sie sichert dem betreffenden Spieler den höchstmöglichen Gewinn, der unabhängig von der Spielweise des Gegners erreichbar ist.

Bei Nicht-Nullsummenspielen, bei denen die Niederlage des Gegners nicht zwangsläufig mit dem eigenen Gewinn zusammenfällt (d.h. Gewinn des einen Spielers $\ne$ Verlust des anderen Spielers), liefert der Minimax-Algorithmus nicht unbedingt eine optimale Strategie.

Spielbaum TTT

Minimax (Idee)

1. Erzeuge kompletten Suchbaum mit Tiefensuche
2. Wende Nutzenfunktion (Utility) auf jeden Endzustand an
3. Ausgehend von Endzuständen => Bewerte Vorgängerknoten:
   • Knoten ist Min-Knoten: Nutzen ist das Minimum der Kindknoten
   • Knoten ist Max-Knoten: Nutzen ist das Maximum der Kindknoten
4. Startknoten: Max wählt den Zug, der zum Nachfolger mit der höchsten Bewertung führt

Annahme: Beide spielen perfekt. Fehler verbessern das Resultat für den Gegner.

Minimax-Algorithmus: Funktionen für MAX- und MIN-Knoten

def Max-Value(state):
    if Terminal-Test(state): return Utility(state)

    v = -INF
    for (a, s) in Successors(state):
        v = MAX(v, Min-Value(s))
    return v

def Min-Value(state):
    if Terminal-Test(state): return Utility(state)

    v = +INF
    for (a, s) in Successors(state):
        v = MIN(v, Max-Value(s))
    return v

Hinweis I: Auf wikipedia.org/wiki/Minimax finden Sie eine Variante mit einem zusätzlichen Tiefenparameter, um bei einer bestimmten Suchtiefe abbrechen zu können. Dies ist bereits eine erweiterte Version, wo man beim Abbruch durch das Erreichen der Suchtiefe statt Utility() eine Eval()-Funktion braucht (vgl. Minimax: Heuristiken).

Wenn man ohne Suchtiefenbeschränkung arbeiten will, braucht man diesen Parameter nicht! Der Algorithmus terminiert auch ohne Suchtiefenbeschränkung!

Hinweis II: Im [Russell2020, S. 196, Abb. 6.3] findet sich eine Variante, die die auf der nächsten Folien gezeigte Startfunktion mit den hier gezeigten Min-Value()- und Max-Value()-Funktionen verschmilzt. Dabei wird in den beiden Hilfsfunktionen nicht nur der min- bzw. max-Wert optimiert, sondern auch der jeweils beste Zug gespeichert und als Rückgabe zurückgeliefert.

Minimax-Algorithmus: Sonderbehandlung Startknoten

def Minimax(state):
    (val, action) = (-INF, null)
    for (a, s) in Successors(state):
        v = Min-Value(s)
        if (val <= v):
            (val, action) = (v, a)
    return action

• Startknoten ist ein MAX-Knoten
• Nicht nur Kosten, sondern auch die zugehörige Aktion speichern

Minimax Beispiel

Aufwand Minimax

• maximale Tiefe des Spielbaums: $m$
• in jedem Zustand $b$ gültige Züge
• => Zeitkomplexität $O(b^m)$

Gedankenexperiment:

• erster Zug: $b$ Möglichkeiten,
• zweiter Zug: jeweils wieder $b$ Möglichkeiten $\rightarrow$ $b \star b = b^2$,
• dritter Zug: jeweils wieder $b$ Möglichkeiten $\rightarrow$ $b \star (b \star b) = b^3$,
• ...,
• $m$. Zug: jeweils wieder $b$ Möglichkeiten $\rightarrow$ $b^m$

Wrap-Up

• Minimax: Entwickelt Spielbaum, bewertet Zustände entsprechend Max und Min
  • Gewinn von Max: +1, Gewinn von Min: -1
  • Max wählt das Maximum der möglichen Züge von Min
  • Min wählt das Minimum der möglichen Züge von Max
  • Spielbaum wird bis zu den Blättern entwickelt, Bewertung mit Utility