NN02 - Lineare Regression und Gradientenabstieg
Videos
Folien
Kurze Übersicht
Formalisierung
- Ausgabe $y$ ist reelle Zahl aus einem stetigen Bereich (zum Beispiel Hauspreis)
- Die Hypothesenfunktion ist eine gewichtete Summe der Merkmale $x_i$ plus eine Konstante $w_0$: $$h(\mathbf{x}) = \mathbf{w}^T\mathbf{x} = w_0 + w_1x_1 + w_2x_2 + \ldots + w_nx_n$$
- Der Verlust (engl. loss) für einen Datenpunkt $\mathbf{x}$ ist das Fehlerquadrat: $$\mathcal{L} = (\hat{y} - y)^2 = (h(\mathbf{x}) - y)^2$$
- Die Kosten (engl. cost) sind der durchschnittliche Verlust über alle Datenpunkte: $$J = \frac{1}{2m} \sum_{i=1}^{m} (\hat{y} - y)^2 = \frac{1}{2m} \sum_{i=1}^{m} (h(\mathbf{x}) - y)^2$$
Der Gradient
- Der Gradientenvektor $\nabla J(\mathbf{w})$ setzt sich zusammen aus den partiellen Ableitungen der Kostenfunktion $J$ nach den Gewichten $w_i$ und zeigt in jedem Punkt $\mathbf{w}$ in die Richtung des steilsten Aufstiegs: $$\nabla J = [ \partial J / \partial w_0 \quad \partial J / \partial w_1 \quad \ldots \quad \partial J / \partial w_n]^T$$
- Schlussfolgerung: In die entgegengesetzte Richtung, i.e. in Richtung $-\nabla J(\mathbf{w})$ geht es am steilsten bergab!
- IDEE: Bewege $\mathbf{w}$ in Richtung $-\nabla J(\mathbf{w})$, um die Kosten $J$ möglichst schnell zu senken.
Der Gradientenabstieg (engl. Gradient Descent)
- Starte mit zufälligen Gewichten $\mathbf{w}$
- Berechne den Gradientenvektor im aktuellen Punkt $\mathbf{w}$
- Gewichtsaktualisierung: Gehe einen kleinen Schritt in Richtung $-\nabla J(\mathbf{w})$ $$\mathbf{w} _{neu} := \mathbf{w} _{alt} - \alpha \cdot \nabla J(\mathbf{w} _{alt})$$ ($\alpha$: Lernrate/Schrittweite).
- Wiederhole Schritte 2-3, bis das globale Minimum von $J$ erreicht ist.
Graphische Übersicht
Übungsblätter/Aufgaben
Lernziele
- (K2) Lineare Regression aus Sicht neuronaler Netze: Graphische Darstellung, Vergleich mit Perzeptron
- (K2) Formalisierung
- (K2) Verlust- und Kostenfunktion
- (K2) Gradientenvektor
- (K2) Lernrate
- (K3) Gradientenabstieg
Challenges
Skalierung der Merkmale
Abbildung 1 und Abbildung 2 zeigen die Höhenlinien (Contour Lines) von zwei Kostenfunktionen.
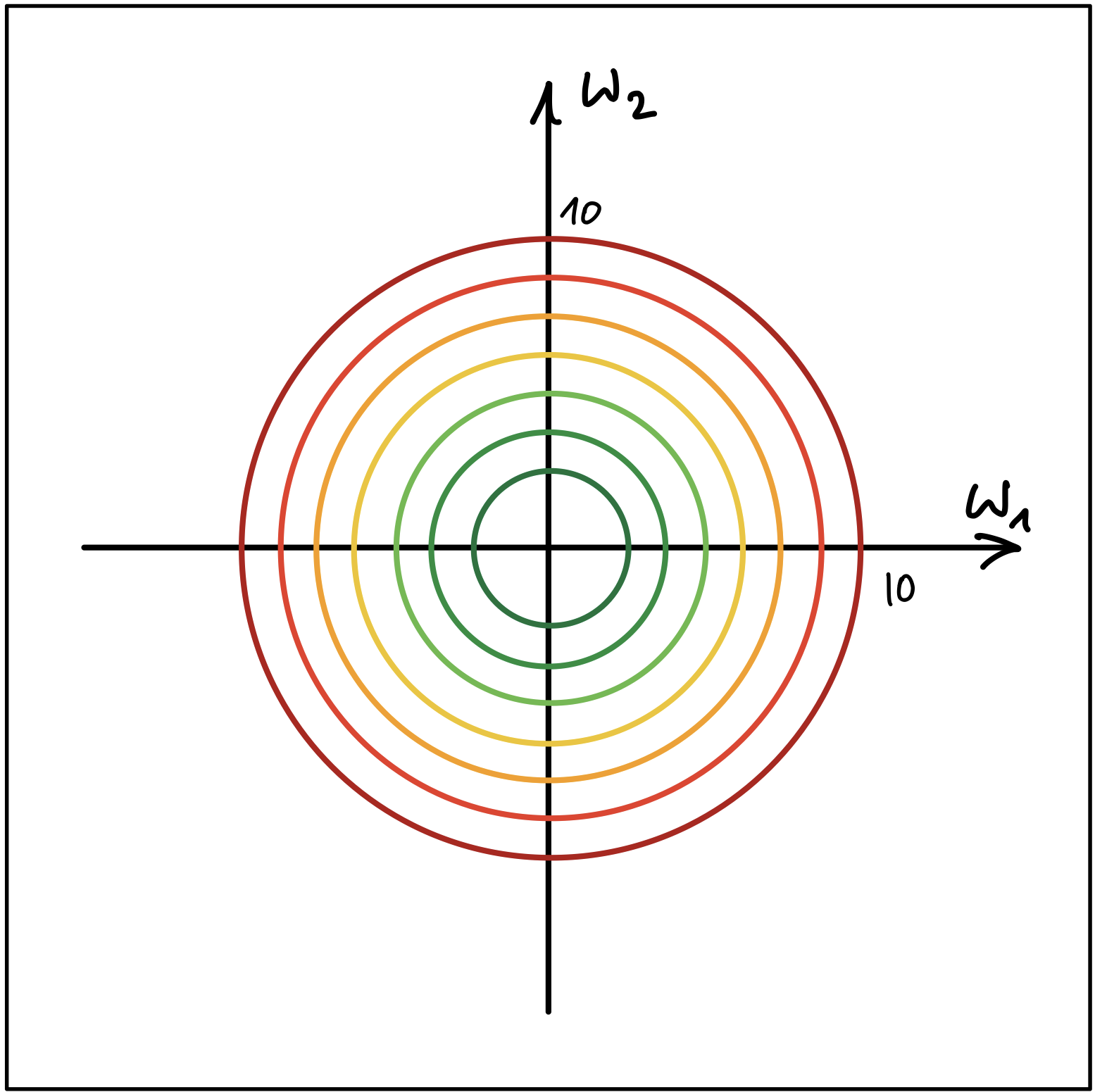
Abbildung 1
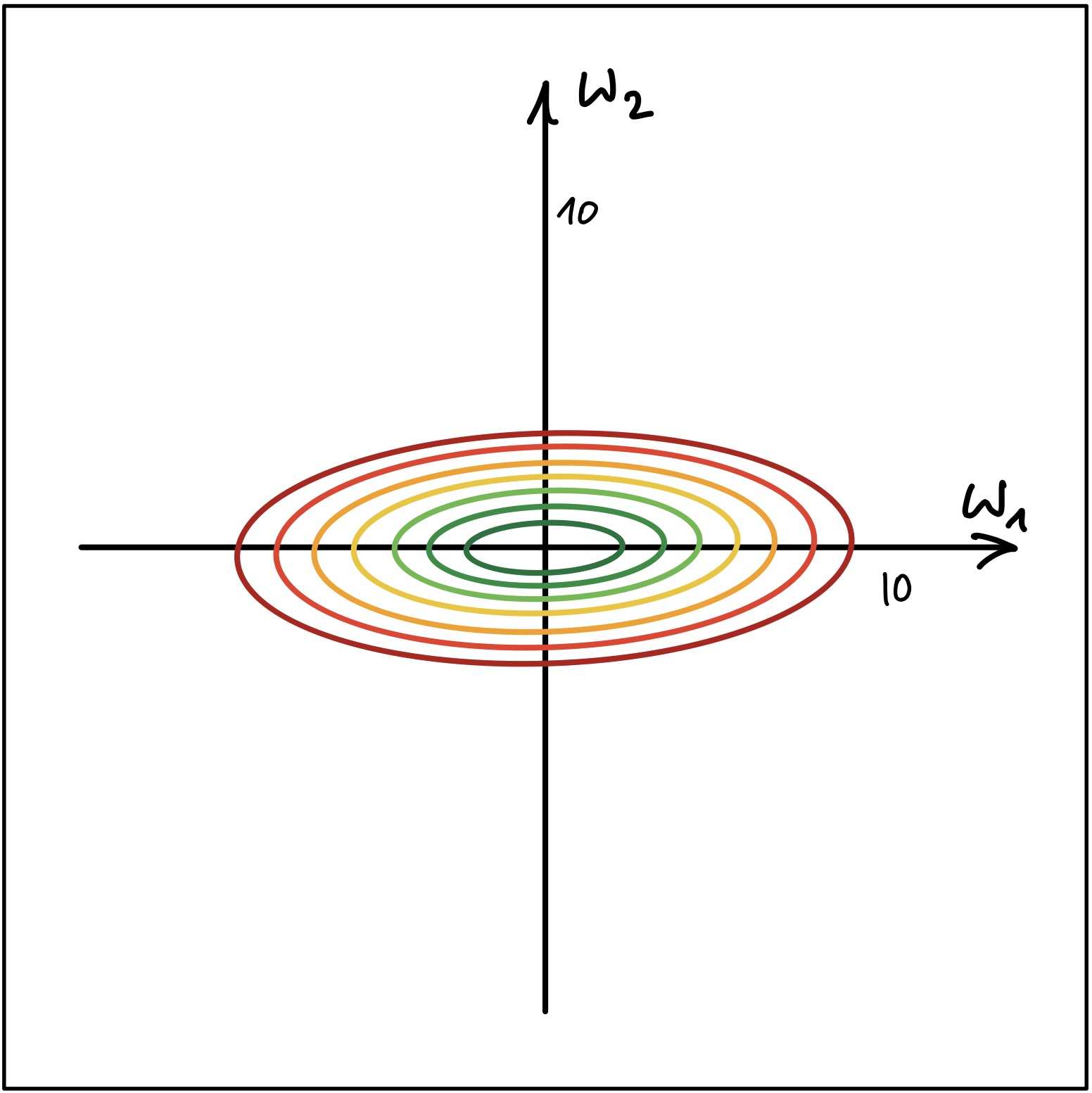
Abbildung 2
- Erklären Sie, welcher der beiden Fälle nachteilhaft für den Gradientenabstieg Algorithmus ist. Wo liegt der Nachteil? Wie kann die Merkmalskalierung dem genannten Nachteil entgegenwirken?
- Zeigen Sie unter Verwendung Ihrer eigenen, zufällig generierten Datenpunkte aus dem Bereich $[100, 300] \times [0, 2]$, wie sich Standardisierung, Min-Max Skalierung und Normalisierung auf die Daten auswirken. Vergleichen Sie dazu die jeweiligen Streudiagramme (scatterplots). Sie können hierzu das folgende Jupyter Notebook als Startpunkt benutzen.

